2008年12月04日 算数数学科研修会 図形の調べ方「証明の導入」
ある中学校で、「証明」の導入部分の授業をみさせていただきました。ともすれば形から入ってしまいがちになる証明の授業ですが、演繹的な推論を通して、証明を概念としてとらえる活動をしていました。
（私も、ともなって変わる量のところで、関数ボックスを使って関数を概念化する授業をしました。）
たとえば「くじら」→「ほ乳類」→「へそがある」という感じです。
非常におもしろい試みだと思いました。ある事柄が正しいことを、筋道を立てて説明することは、日常生活や、社会に出たとき、とても役に立つことなので、本当は本時のように概念的なものからはいるのが理想的だと思います。しかし、形から入って数をこなし、証明になれることを通して概念に気づいていく場合もあります。私の場合、時間的なことを考えると、ついつい概念をおろそかにしてしまい、型にはめて証明を覚えさせてしまうことが多いのですが、本時のように最初に証明とはどういうものなのかに演繹的に触れることは、概念を形成するための一つの手段として有効だなと思いました。
 図形の証明の導入部分の指導案を集めてみました。
・ 三角形の合同条件と証明の進め方 (埼玉県立総合教育センター）
平行四辺形になるための条件
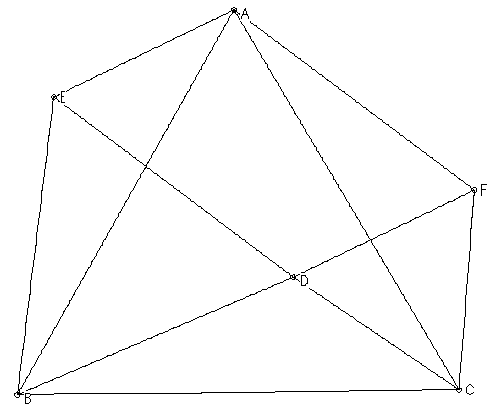
本時は下記の「四角形ＡＥＤＦが平行四辺形になることを証明する」ために、コンピュータソフト「図形ランチボックス３」を使用して授業を実施しました。
前時に学習した「平行四辺形になるための条件」を使って、図形の性質を確かめる活動の最終段階なので、図形の観察や操作的活動による思考を重視し、生徒の興味・関心を引くような指導を心がけた。
導入では簡単な図形を作図させ、自分が書いた図形を観察し、特定の１点を頭の中で動かすことによって、図形がどのように変化するのか予想させた。そして、思考だけでは計り知れない部分を、コンピュータを使って実際に点を動かしてみることにより検証し、確かなイメージとして感じ取らせた
。また、この作業により気付いたことを、すべての図形について説明するのが難しいことに着目させ、証明の必要性に気付かせると同時に、そのよさ
が実感できたようである。
△ＡＢＣ、△ＥＢＤ、△ＦＤＣは正三角形
|
正の数・負の数